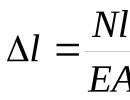Huko dėsnis, atsižvelgiant į temperatūros įtempius. Deformacijos ir judesiai. Huko dėsnis. Huko dėsnis matematine forma
8.2. Pagrindiniai medžiagų stiprumo dėsniai
Statiniai santykiai. Jos parašytos šių pusiausvyros lygčių forma.
Huko dėsnis ( 1678): kuo didesnė jėga, tuo didesnė deformacija, be to, ji yra tiesiogiai proporcinga jėgai. Fiziškai tai reiškia, kad visi kūnai yra spyruoklės, bet labai tvirti. Kai sija tiesiog ištempiama išilgine jėga N= Fšis įstatymas gali būti parašytas taip:
Čia 
išilginė jėga, l- sijos ilgis, A- jo skerspjūvio plotas, E- pirmos rūšies elastingumo koeficientas ( Youngo modulis).
Atsižvelgiant į įtempių ir deformacijų formules, Huko dėsnis parašytas taip: 
.
Panašus ryšys stebimas atliekant eksperimentus tarp tangentinių įtempių ir šlyties kampo:
.
G
paskambinošlyties modulis
, rečiau – antros rūšies tamprumo modulis. Kaip ir bet kuris įstatymas, Huko dėsnis taip pat turi taikymo ribą. Įtampa 
, iki kurios galioja Huko dėsnis, vadinamas proporcingumo riba(tai yra svarbiausia medžiagų stiprumo charakteristika).
Pavaizduokime priklausomybę
iš
grafiškai (8.1 pav.). Šis paveikslas vadinamas tempimo diagrama
. Po taško B (t. y 
) ši priklausomybė nustoja būti tiesinė.
At 
iškrovus kūne atsiranda liekamųjų deformacijų, todėl 
paskambino elastingumo riba
.
Kai įtampa pasiekia reikšmę σ = σ t, daugelis metalų pradeda turėti savybę, vadinamą sklandumas. Tai reiškia, kad net esant nuolatinei apkrovai medžiaga ir toliau deformuojasi (tai yra, ji elgiasi kaip skystis). Grafiškai tai reiškia, kad diagrama yra lygiagreti abscisei (DL atkarpa). Vadinama įtampa σ t, kuria teka medžiaga takumo stiprumas .
Kai kurios medžiagos (St. 3 – statybinis plienas) po trumpo tekėjimo vėl pradeda priešintis. Medžiagos atsparumas tęsiasi iki tam tikros didžiausios vertės σ pr, tada prasideda laipsniškas sunaikinimas. Vadinamas dydis σ pr atsparumas tempimui (plieno sinonimas: atsparumas tempimui, betonui - kubinis arba prizminis stiprumas). Taip pat naudojami šie pavadinimai:
=R b
Panašus ryšys stebimas atliekant eksperimentus tarp šlyties įtempių ir kirpimų.
3) Duhamelio – Neumano dėsnis (tiesinis šiluminis plėtimasis):
Esant temperatūrų skirtumui, kūnai keičia savo dydį ir tiesiogiai proporcingai šiam temperatūros skirtumui.
Tegul būna temperatūros skirtumas 
. Tada šis įstatymas atrodo taip:
Čia α - linijinio šiluminio plėtimosi koeficientas, l - strypo ilgis, Δ l- jo pailgėjimas.
4) Šliaužimo dėsnis .
Tyrimai parodė, kad visos medžiagos yra labai nevienalytės mažuose plotuose. Plieno schema pavaizduota 8.2 pav.
Kai kurie komponentai turi skysčio savybių, todėl daugelis apkrovos medžiagų laikui bėgant papildomai pailgėja 
(8.3 pav.) (metalai aukštoje temperatūroje, betonas, mediena, plastikai – normalioje temperatūroje). Šis reiškinys vadinamas šliaužti medžiaga.
Skysčių įstatymas yra toks: kuo didesnė jėga, tuo didesnis kūno judėjimo greitis skystyje. Jei šis ryšys yra tiesinis (ty jėga proporcinga greičiui), tada jį galima parašyti taip:
E 
Jei pereisime prie santykinių jėgų ir santykinių pailgėjimų, gausime
Čia yra rodyklė " kr
"reiškia, kad atsižvelgiama į pailgėjimo dalį, kurią sukelia medžiagos šliaužimas. Mechaninės charakteristikos 
vadinamas klampos koeficientu.
Energijos tvermės dėsnis.
Apsvarstykite apkrautą spindulį
Pavyzdžiui, pristatykime taško perkėlimo sąvoką,
- vertikalus taško B judėjimas;
- taško C horizontalus poslinkis.
Galios 
dirbdamas kokį nors darbą U.
Atsižvelgiant į tai, kad jėgos 
pradeda palaipsniui didėti ir darant prielaidą, kad jie didėja proporcingai poslinkiams, gauname:
.
Pagal gamtosaugos įstatymą: joks darbas nedingsta, jis eikvojamas kitam darbui arba virsta kita energija (energijos– tai darbas, kurį gali atlikti kūnas.).
Jėgų darbas 
, išleidžiama mūsų kūne kylančių tamprumo jėgų pasipriešinimui įveikti. Norėdami apskaičiuoti šį darbą, atsižvelgiame į tai, kad kūnas gali būti sudarytas iš mažų elastingų dalelių. Panagrinėkime vieną iš jų:
Jį veikia gretimų dalelių įtampa 
. Atsiras stresas 
Esant įtakai 
dalelė pailgės. Pagal apibrėžimą pailgėjimas yra ilgio vieneto pailgėjimas. Tada:
Paskaičiuokime darbą dW, kurią daro jėga dN (čia taip pat atsižvelgiama į tai, kad jėgos dN pradeda palaipsniui didėti ir didėja proporcingai judesiams):
Visam kūnui gauname:
.
Darbas W kuris buvo įvykdytas 
, paskambino elastinės deformacijos energija.
Pagal energijos tvermės dėsnį:
6)Principas galimi judesiai .
Tai vienas iš energijos tvermės dėsnio rašymo variantų.
Tegul jėgos veikia siją F 1
,
F 2
,
…
. Jie sukelia taškų judėjimą kūne 
ir įtampa 
. Duokime kūną papildomi nedideli galimi judesiai
. Mechanikoje formos žymėjimas 
reiškia frazę „galima kiekio vertė A“ Šie galimi judesiai sukels kūną papildomos galimos deformacijos
. Jie sukels papildomų išorinių jėgų ir įtempių atsiradimą 
,
δ.
Apskaičiuokime išorinių jėgų darbą esant papildomiems galimiems mažiems poslinkiams:
Čia 
- papildomi judesiai tų taškų, kuriuose veikia jėgos F 1
,
F 2
,
…
Dar kartą apsvarstykite nedidelį skerspjūvio elementą dA ir ilgis dz (žr. 8.5. ir 8.6 pav.). Pagal apibrėžimą papildomas pailgėjimas dzŠio elemento kiekis apskaičiuojamas pagal formulę:
dz= dz.
Elemento tempimo jėga bus tokia:
dN = (+δ) dA ≈ dA..
Vidinių jėgų darbas esant papildomiems poslinkiams mažam elementui apskaičiuojamas taip:
dW = dN dz = dA dz = dV
SU 
Susumavus visų mažų elementų deformacijos energiją gauname bendrą deformacijos energiją:
Energijos tvermės dėsnis W = U suteikia:
.
Šis santykis vadinamas galimų judesių principas(taip pat vadinamas virtualių judesių principas). Panašiai galime apsvarstyti atvejį, kai veikia ir tangentiniai įtempiai. Tada mes galime gauti tai iki deformacijos energijos W bus pridėtas šis terminas:
Čia yra šlyties įtempis, yra mažojo elemento poslinkis. Tada galimų judesių principas bus tokia forma:
Skirtingai nuo ankstesnės energijos tvermės dėsnio rašymo formos, čia nėra prielaidos, kad jėgos pradeda didėti palaipsniui, o didėja proporcingai poslinkiams.
7) Poisson efektas.
Panagrinėkime mėginio pailgėjimo modelį:
Kūno elemento sutrumpėjimo pailgėjimo kryptimi reiškinys vadinamas Poisson efektas.
Raskime išilginę santykinę deformaciją.
Skersinė santykinė deformacija bus:
Puasono koeficientas kiekis vadinamas:
Izotropinėms medžiagoms (plienui, ketui, betonui) Puasono santykis
Tai reiškia, kad skersine kryptimi deformacija mažiau išilginis
Pastaba
: šiuolaikinėmis technologijomis galima sukurti kompozitines medžiagas, kurių Puasono koeficientas >1, tai yra, skersinė deformacija bus didesnė nei išilginė. Pavyzdžiui, tai pasakytina apie medžiagą, sustiprintą standiais pluoštais mažu kampu 
<<1
(см. рис.8.8.). Оказывается, что коэффициент
Пуассона при этом почти пропорционален
величине
, t.y. tuo mažiau 
, tuo didesnis Puasono koeficientas.
8.8 pav. 8.9 pav
Dar labiau stebina medžiaga, parodyta (8.9 pav.), o tokiam sutvirtinimui yra paradoksalus rezultatas - išilginis pailgėjimas lemia kūno dydžio padidėjimą skersine kryptimi.
8) Apibendrintas Huko dėsnis.
Panagrinėkime elementą, kuris tęsiasi išilgine ir skersine kryptimis. Raskime deformaciją, kuri atsiranda šiomis kryptimis. 
Apskaičiuokime deformaciją 
kylančių iš veiksmo 
:
Panagrinėkime deformaciją nuo veiksmo 
, kuris atsiranda dėl Puasono efekto:
Bendra deformacija bus tokia:
Jei galioja ir 
, tada bus pridėtas dar vienas sutrumpinimas x ašies kryptimi 
.
Taigi: 
Taip pat: 
Šie santykiai vadinami apibendrintas Huko dėsnis.
Įdomu tai, kad rašant Huko dėsnį daroma prielaida apie pailgėjimo deformacijų nepriklausomumą nuo šlyties deformacijų (apie nepriklausomumą nuo šlyties įtempių, tai yra tas pats) ir atvirkščiai. Eksperimentai gerai patvirtina šias prielaidas. Žvelgdami į ateitį, pastebime, kad stiprumas, priešingai, labai priklauso nuo tangentinių ir normalių įtempių derinio.
Pastaba: Minėtus dėsnius ir prielaidas patvirtina daugybė tiesioginių ir netiesioginių eksperimentų, tačiau, kaip ir visi kiti dėsniai, jų taikymo sritis yra ribota.
Huko dėsnį XVII amžiuje atrado anglas Robertas Hukas. Šis atradimas apie spyruoklės tempimą yra vienas iš elastingumo teorijos dėsnių ir vaidina svarbų vaidmenį moksle ir technikoje.
Huko dėsnio apibrėžimas ir formulė
Šio dėsnio formuluotė yra tokia: tamprumo jėga, atsirandanti kūno deformacijos momentu, yra proporcinga kūno pailgėjimui ir yra nukreipta priešingai šio kūno dalelių judėjimui kitų dalelių atžvilgiu deformacijos metu.
Matematinė įstatymo žyma atrodo taip:
Ryžiai. 1. Huko dėsnio formulė
Kur Fupr– atitinkamai tamprumo jėga, x– kūno pailgėjimas (atstumas, kuriuo keičiasi pradinis kūno ilgis), ir k– proporcingumo koeficientas, vadinamas kūno standumu. Jėga matuojama niutonais, o kūno pailgėjimas – metrais.
Norėdami atskleisti fizinę standumo reikšmę, Huko dėsnio formulėje turite pakeisti vienetą, kuriame matuojamas pailgėjimas - 1 m, prieš tai gavę k išraišką.
Ryžiai. 2. Kūno standumo formulė
Ši formulė rodo, kad kūno standumas skaitine prasme yra lygus tamprumo jėgai, kuri atsiranda kūne (spyruokle), kai jis deformuojamas 1 m. Yra žinoma, kad spyruoklės standumas priklauso nuo jos formos, dydžio ir medžiagos. iš kurių pagamintas kūnas.
Elastinė jėga
Dabar, kai žinome, kokia formulė išreiškia Huko dėsnį, būtina suprasti pagrindinę jo reikšmę. Pagrindinis dydis yra tamprumo jėga. Jis atsiranda tam tikru momentu, kai kūnas pradeda deformuotis, pavyzdžiui, suspaudus ar ištempus spyruoklę. Jis nukreiptas priešinga gravitacijos kryptimi. Kai tampriosios jėgos ir kūną veikiančios gravitacijos jėgos tampa vienodos, atrama ir kūnas sustoja.
Deformacija yra negrįžtamas kūno dydžio ir formos pokytis. Jie yra susiję su dalelių judėjimu viena kitos atžvilgiu. Jei žmogus sėdi minkštoje kėdėje, tada kėdė deformuojasi, tai yra, pasikeis jos savybės. Jis būna įvairių tipų: lenkimo, tempimo, suspaudimo, šlyties, sukimo.
Kadangi tamprumo jėga yra kilmė susijusi su elektromagnetinėmis jėgomis, turėtumėte žinoti, kad ji atsiranda dėl to, kad molekulės ir atomai - mažiausios dalelės, sudarančios visus kūnus - traukia ir atstumia vienas kitą. Jei atstumas tarp dalelių yra labai mažas, tada jas veikia atstūmimo jėga. Jei šis atstumas padidės, tada juos veiks traukos jėga. Taigi skirtumas tarp patrauklių ir atstumiančių jėgų pasireiškia tamprumo jėgomis.
Tamprioji jėga apima žemės reakcijos jėgą ir kūno svorį. Ypač domina reakcijos stiprumas. Tai jėga, kuri veikia kūną, kai jis yra ant bet kokio paviršiaus. Jei kūnas pakabinamas, tai jį veikianti jėga vadinama sriegio įtempimo jėga.
Tamprumo jėgų ypatumai
Kaip jau išsiaiškinome, deformacijos metu atsiranda tamprumo jėga, kuria siekiama atkurti pirmines formas ir dydžius griežtai statmenai deformuotam paviršiui. Tamprios jėgos taip pat turi keletą savybių.
- jie atsiranda deformacijos metu;
- jie vienu metu atsiranda dviejuose deformuojamuose kūnuose;
- jie yra statmeni paviršiui, kurio atžvilgiu kūnas deformuojamas.
- jos yra priešingos kūno dalelių poslinkio kryptimi.
Teisės taikymas praktikoje
Huko dėsnis taikomas tiek techniniuose, tiek aukštųjų technologijų įrenginiuose, tiek pačioje gamtoje. Pavyzdžiui, tamprumo jėgos yra laikrodžių mechanizmuose, amortizatoriuose transporte, virvėse, guminėse juostose ir net žmonių kauluose. Huko dėsnio principas grindžiamas dinamometru – prietaisu, naudojamu jėgai matuoti.
Krymo autonominės Respublikos švietimo ministerija
Tauride nacionalinis universitetas pavadintas. Vernadskis
Fizinės teisės studijos
HOKO dėsnis
Baigė: 1 kurso studentas
Fizikos fakulteto gr. F-111
Potapovas Jevgenijus
Simferopolis-2010 m
Planas:
Ryšys tarp kokių reiškinių ar dydžių išreiškiamas dėsniu.
Įstatymo pareiškimas
Matematinė dėsnio išraiška.
Kaip dėsnis buvo atrastas: remiantis eksperimentiniais duomenimis ar teoriškai?
Patirti faktai, kurių pagrindu buvo suformuluotas įstatymas.
Teorijos pagrindu suformuluoto dėsnio pagrįstumą patvirtinantys eksperimentai.
Įstatymo panaudojimo ir atsižvelgimo į įstatymo poveikį praktikoje pavyzdžiai.
Literatūra.
Santykis tarp reiškinių ar dydžių išreiškiamas įstatymu:
Huko dėsnis susijęs su tokiais reiškiniais kaip įtempis ir kietojo kūno tamprumo modulio deformacija ir pailgėjimas. Kūno deformacijos metu atsirandančios tamprumo jėgos modulis yra proporcingas jo pailgėjimui. Pailgėjimas yra medžiagos deformuojamumo charakteristika, įvertinama pagal šios medžiagos pavyzdžio ilgį ištempus. Tamprioji jėga yra jėga, kuri atsiranda deformuojantis kūnui ir neutralizuoja šią deformaciją. Įtampa yra vidinių jėgų, atsirandančių deformuojamame kūne, veikiant išoriniams poveikiams, matas. Deformacija – tai kūno dalelių santykinės padėties pasikeitimas, susijęs su jų judėjimu viena kitos atžvilgiu. Šios sąvokos yra susijusios su vadinamuoju standumo koeficientu. Tai priklauso nuo medžiagos elastingumo savybių ir korpuso dydžio.
Įstatymo teiginys:
Huko dėsnis yra elastingumo teorijos lygtis, susiejanti tamprios terpės įtempį ir deformaciją.
Dėsnio formuluotė yra tokia, kad tamprumo jėga yra tiesiogiai proporcinga deformacijai.
Matematinė dėsnio išraiška:
Plono tempimo strypo atveju Huko dėsnis yra toks:
Čia F strypo įtempimo jėga, Δ l- jo pailgėjimas (suspaudimas) ir k paskambino elastingumo koeficientas(arba standumas). Minusas lygtyje rodo, kad įtempimo jėga visada nukreipta deformacijai priešinga kryptimi.
Jei įvesite santykinį pailgėjimą
ir normalus įtempis skerspjūvyje
tada Huko dėsnis bus parašytas taip
Šioje formoje jis galioja bet kokiems mažiems medžiagos kiekiams.
Bendru atveju įtempis ir deformacija yra antrojo rango tenzoriai trimatėje erdvėje (jie turi po 9 komponentus). Jas jungiančių tamprių konstantų tenzorius yra ketvirtos eilės tenzorius C ijkl ir jame yra 81 koeficientas. Dėl tenzoriaus simetrijos C ijkl, taip pat įtempių ir deformacijų tenzoriai, tik 21 konstanta yra nepriklausoma. Huko dėsnis atrodo taip:
kur σ ij- įtempių tenzoras, - įtempių tenzorius. Izotropinei medžiagai tenzorius C ijkl yra tik du nepriklausomi koeficientai.
Kaip įstatymas buvo atrastas: remiantis eksperimentiniais duomenimis ar teoriškai:
Įstatymą 1660 metais atrado anglų mokslininkas Robertas Hukas (Kablys), remdamasis stebėjimais ir eksperimentais. Atradimą, kaip teigia Hooke'as savo esė „De potentia restitutiva“, išleistoje 1678 m., jis padarė 18 metų anksčiau, o 1676 m. jis buvo įtrauktas į kitą jo knygą, prisidengdamas anagrama „ceiiinosssttuv“, reiškiančia. „Ut tensio sic vis“. Minėtas proporcingumo dėsnis, autoriaus paaiškinimu, galioja ne tik metalams, bet ir medžiui, akmenims, ragui, kaulams, stiklui, šilkui, plaukams ir kt.
Patirti faktai, kurių pagrindu buvo suformuluotas įstatymas:
Istorija apie tai tyli..
Eksperimentai, patvirtinantys teorijos pagrindu suformuluoto įstatymo pagrįstumą:
Įstatymas suformuluotas remiantis eksperimentiniais duomenimis. Išties, tempiant kūną (viela) su tam tikru standumo koeficientu k iki atstumo Δ l, tada jų sandauga bus lygi kūno (vielos) tempimo jėgai. Tačiau šis santykis galioja ne visoms deformacijoms, o mažoms. Esant didelėms deformacijoms, Huko dėsnis nustoja galioti ir kūnas griūva.
Įstatymo naudojimo ir atsižvelgimo į įstatymo poveikį praktikoje pavyzdžiai:
Kaip matyti iš Huko dėsnio, pagal spyruoklės pailgėjimą galima spręsti apie ją veikiančią jėgą. Šis faktas naudojamas jėgoms matuoti naudojant dinamometrą – spyruoklę su linijine skale, kalibruota skirtingoms jėgos vertėms.
Literatūra.
1. Interneto ištekliai: - Vikipedijos svetainė (http://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%93%D1%83 % D0%BA%D0%B0).
2. fizikos vadovėlis Peryshkin A.V. 9 klasė
3. fizikos vadovėlis V.A. Kasjanovas 10 klasė
4. paskaitos apie mechaniką Ryabushkin D.S.
Huko dėsnis paprastai vadinami tiesiniais ryšiais tarp deformacijos komponentų ir įtempių komponentų.
Paimkime elementarų stačiakampį gretasienį, kurio paviršiai lygiagrečiai koordinačių ašims, apkrautą normaliu įtempimu σ x, tolygiai paskirstytas dviejuose priešinguose paviršiuose (1 pav.). Kuriame σy = σ z = τ x y = τ x z = τ yz = 0.
Iki proporcingumo ribos santykinis pailgėjimas nurodomas formule
Kur E— tamprumo tempimo modulis. Dėl plieno E = 2*10 5 MPa, todėl deformacijos yra labai mažos ir matuojamos procentais arba 1 * 10 5 (deformacijos matavimo prietaisuose).
Elemento išplėtimas ašies kryptimi X kartu su jo susiaurėjimu skersine kryptimi, nulemtu deformacijos komponentų
Kur μ - konstanta, vadinama šoniniu suspaudimo laipsniu arba Puasono koeficientu. Dėl plieno μ paprastai imamas 0,25-0,3.
Jei aptariamas elementas apkraunamas kartu su normaliais įtempiais σ x, σy, σ z, tolygiai paskirstytas išilgai jo paviršių, tada pridedamos deformacijos
Sudėjus deformacijos komponentus, kuriuos sukelia kiekvienas iš trijų įtempių, gauname ryšius
Šiuos ryšius patvirtina daugybė eksperimentų. Taikoma perdangos metodas arba superpozicijos kelių jėgų sukeltų suminių deformacijų ir įtempių nustatymas yra teisėtas tol, kol deformacijos ir įtempimai yra maži ir tiesiškai priklauso nuo taikomų jėgų. Tokiais atvejais neatsižvelgiame į nedidelius deformuoto kūno matmenų pokyčius ir nedidelius išorinių jėgų taikymo taškų judesius ir skaičiuodami remiamės pradiniais kūno matmenimis ir pradine forma.
Reikia pažymėti, kad poslinkių mažumas nebūtinai reiškia, kad jėgų ir deformacijų santykiai yra tiesiniai. Taigi, pavyzdžiui, suspaustoje jėgoje K strypas papildomai apkrautas šlyties jėga R, net ir esant nedideliam įlinkiui δ atsiranda papildomas taškas M = Qδ, todėl problema yra netiesinė. Tokiais atvejais suminiai įlinkiai nėra tiesinės jėgų funkcijos ir negali būti gaunami naudojant paprastą superpoziciją.
Eksperimentiškai nustatyta, kad jei šlyties įtempiai veikia išilgai visų elemento paviršių, tai atitinkamo kampo iškraipymas priklauso tik nuo atitinkamų šlyties įtempių komponentų.
Pastovus G vadinamas šlyties tamprumo moduliu arba šlyties moduliu.
Bendras elemento deformacijos atvejis dėl trijų normalių ir trijų tangentinių įtempių komponentų poveikio gali būti gautas naudojant superpoziciją: trys šlyties deformacijos, nustatytos ryšiais (5.2b), dedamos ant trijų tiesinių deformacijų, nustatytų išraiškomis ( 5.2a). Lygtys (5.2a) ir (5.2b) nustato ryšį tarp deformacijų ir įtempių komponentų ir yra vadinamos apibendrintas Huko dėsnis. Dabar parodykime, kad šlyties modulis G išreikštas tamprumo tempimo moduliu E ir Puasono koeficientas μ . Norėdami tai padaryti, apsvarstykite ypatingą atvejį, kai σ x = σ , σy = -σ Ir σ z = 0.
Iškirpkime elementą abcd plokštumos lygiagrečios ašiai z ir pasviręs 45° kampu ašių atžvilgiu X Ir adresu(3 pav.). Kaip matyti iš 0 elemento pusiausvyros sąlygų bс, normalus stresas σ v visuose elemento paviršiuose abcd yra lygūs nuliui, o šlyties įtempiai yra lygūs
Tokia įtampos būsena vadinama grynas kirpimas. Iš (5.2a) lygčių išplaukia, kad
tai yra, horizontalaus elemento išplėtimas yra 0 c lygus vertikalaus elemento sutrumpėjimui 0 b: εy = -εx.
Kampas tarp veidų ab Ir bc pokyčius ir atitinkamą šlyties deformacijos vertę γ galima rasti iš trikampio 0 bс:
Tai seka
Išorinių jėgų poveikis kietam kūnui lemia įtempių ir deformacijų atsiradimą jo tūrio taškuose. Šiuo atveju įtempimo būsena taške, santykis tarp įtempių įvairiose srityse, einančiose per šį tašką, yra nustatomas pagal statikos lygtis ir nepriklauso nuo medžiagos fizikinių savybių. Deformuota būsena, santykis tarp poslinkių ir deformacijų, nustatomas remiantis geometriniais ar kinematine svarstymais ir taip pat nepriklauso nuo medžiagos savybių. Norint nustatyti ryšį tarp įtempių ir deformacijų, būtina atsižvelgti į faktines medžiagos savybes ir apkrovos sąlygas. Remiantis eksperimentiniais duomenimis, sukurti matematiniai modeliai, apibūdinantys įtempių ir deformacijų ryšius. Šie modeliai turi pakankamai tiksliai atspindėti faktines medžiagų savybes ir apkrovos sąlygas.
Labiausiai paplitę konstrukcinių medžiagų modeliai yra elastingumas ir plastiškumas. Elastingumas – tai kūno savybė, veikiant išorinėms apkrovoms, pakeisti formą ir dydį, o pašalinus apkrovą atkurti pradinę konfigūraciją. Matematiškai elastingumo savybė išreiškiama nustatant funkcinį ryšį vienas su vienu tarp įtempių tenzoriaus ir deformacijos tenzoriaus komponentų. Elastingumo savybė atspindi ne tik medžiagų savybes, bet ir apkrovos sąlygas. Daugumos konstrukcinių medžiagų elastingumo savybė pasireiškia esant vidutinėms išorinių jėgų vertėms, sukeliančioms mažas deformacijas, ir esant mažam apkrovos greičiui, kai energijos nuostoliai dėl temperatūros poveikio yra nereikšmingi. Medžiaga vadinama tiesiškai elastinga, jei įtempių tenzoriaus ir deformacijos tenzoriaus komponentai yra susiję tiesiniais ryšiais.
Esant dideliems apkrovų lygiams, atsiradus reikšmingoms kūno deformacijoms, medžiaga iš dalies praranda savo elastines savybes: iškraunant jos pirminiai matmenys ir forma visiškai neatkuriami, o visiškai pašalinus išorines apkrovas, fiksuojamos liekamosios deformacijos. Tokiu atveju ryšys tarp įtempių ir deformacijų nustoja būti vienareikšmis. Ši materialinė savybė vadinama plastiškumas. Plastinės deformacijos metu susikaupusios liekamosios deformacijos vadinamos plastinėmis.
Didelė apkrova gali sukelti destrukcija, t.y. kūno padalijimas į dalis. Kietosios medžiagos, pagamintos iš skirtingų medžiagų, sugenda esant skirtingam deformacijos dydžiui. Lūžis yra trapus esant mažoms deformacijoms ir paprastai vyksta be pastebimų plastinių deformacijų. Toks sunaikinimas būdingas ketui, legiruotam plienui, betonui, stiklui, keramikai ir kai kurioms kitoms konstrukcinėms medžiagoms. Mažai anglies dioksido išskiriantis plienas, spalvotieji metalai ir plastikai pasižymi plastišku gedimu, kai yra didelės liekamosios deformacijos. Tačiau medžiagų skirstymas į trapias ir plastiškas pagal jų sunaikinimo pobūdį yra labai savavališkas, paprastai tai susiję su kai kuriomis standartinėmis eksploatavimo sąlygomis. Ta pati medžiaga, priklausomai nuo sąlygų (temperatūros, apkrovos pobūdžio, gamybos technologijos ir kt.), gali būti trapi arba plastiška. Pavyzdžiui, medžiagos, kurios normalioje temperatūroje yra plastikinės, žemoje temperatūroje skyla kaip trapios. Todėl teisingiau kalbėti ne apie trapias ir plastikines medžiagas, o apie trapią ar plastišką medžiagos būklę.
Tegul medžiaga yra tiesiškai elastinga ir izotropinė. Nagrinėkime elementarųjį tūrį vienaašės įtempimo būsenos sąlygomis (1 pav.), kad įtempių tenzorius turėtų formą
Esant tokiai apkrovai, matmenys didėja ašies kryptimi Oi, būdinga tiesine deformacija, kuri yra proporcinga įtempių dydžiui
1 pav. Vienaašė įtempio būsena
Šis ryšys yra matematinis žymėjimas Huko dėsnis nustatantis proporcingą ryšį tarp įtempių ir atitinkamos tiesinės deformacijos vienaašėje įtempių būsenoje. Proporcingumo koeficientas E vadinamas išilginiu tamprumo moduliu arba Youngo moduliu. Jis turi streso dimensiją.
Kartu su dydžio padidėjimu veiksmų kryptimi; Esant tokiam pat įtempimui, dydis mažėja dviem statmenomis kryptimis (1 pav.). Atitinkamas deformacijas žymime ir , ir šios deformacijos yra neigiamos, o teigiamos ir yra proporcingos:
Vienu metu veikiant įtempiams išilgai trijų stačiakampių ašių, kai nėra tangentinių įtempių, tiesiškai elastingai medžiagai galioja superpozicijos (sprendinių superpozicijos) principas:
Atsižvelgdami į formules (1 4) gauname
|
Tangentiniai įtempiai sukelia kampines deformacijas, o esant mažoms deformacijoms jie neturi įtakos linijinių matmenų pokyčiui, taigi ir tiesinėms deformacijoms. Todėl jie galioja ir esant savavališkai įtempių būsenai ir išreiškia vadinamąją apibendrintas Huko dėsnis.
Kampinę deformaciją sukelia tangentinis įtempis, o deformacija ir atitinkamai įtempiai ir. Yra proporcingi ryšiai tarp atitinkamų tangentinių įtempių ir kampinių deformacijų tiesiškai elastingam izotropiniam kūnui
kurios išreiškia teisę Huko žirklės. Proporcingumo koeficientas G vadinamas šlyties modulis. Svarbu, kad normalus įtempis neturėtų įtakos kampinėms deformacijoms, nes tokiu atveju keičiasi tik atkarpų linijiniai matmenys, o ne kampai tarp jų (1 pav.).
Taip pat egzistuoja tiesinis ryšys tarp vidutinio įtempio (2.18), proporcingo pirmajam įtempio tenzoriaus invariantui, ir tūrinės deformacijos (2.32), sutampančiu su pirmuoju deformacijos tenzoriaus invariantu:
2 pav. Plokštumos šlyties deformacija
Atitinkamas proporcingumo koeficientas KAM paskambino tūrinis tamprumo modulis.
Formulės (1 7) apima medžiagos elastingumo charakteristikas E, , G Ir Į, nustatant jo elastines savybes. Tačiau šios savybės nėra nepriklausomos. Izotropinei medžiagai yra dvi nepriklausomos tamprumo charakteristikos, kurios dažniausiai pasirenkamos kaip tamprumo modulis E ir Puasono koeficientas. Šlyties moduliui išreikšti G per E Ir , Panagrinėkime plokštumos šlyties deformaciją veikiant tangentiniams įtempiams (2 pav.). Norėdami supaprastinti skaičiavimus, naudojame kvadratinį elementą su šonine A. Apskaičiuokime pagrindinius įtempius , . Šie įtempiai veikia sritis, esančias kampu į pradines sritis. Iš pav. 2 rasime ryšį tarp tiesinės deformacijos įtempių kryptimi ir kampinės deformacijos . Didžioji rombo įstrižainė, apibūdinanti deformaciją, lygi
Mažoms deformacijoms
Atsižvelgiant į šiuos santykius
Prieš deformaciją ši įstrižainė turėjo tokio dydžio . Tada turėsime
Iš apibendrinto Huko dėsnio (5) gauname
Gautos formulės palyginimas su Huko dėsnio poslinkiui (6) žymėjimu duoda
Kaip rezultatas, mes gauname
Palyginę šią išraišką su Huko tūriniu dėsniu (7), gauname rezultatą
Mechaninės charakteristikos E, , G Ir KAM randami apdorojus eksperimentinius duomenis, gautus tiriant mėginius esant įvairioms apkrovoms. Fiziniu požiūriu visos šios savybės negali būti neigiamos. Be to, iš paskutinės išraiškos matyti, kad Puasono santykis izotropinei medžiagai neviršija 1/2. Taigi gauname šiuos izotropinės medžiagos tamprumo konstantų apribojimus:
Ribinė vertė veda prie ribinės vertės , kuri atitinka nesuspaudžiamą medžiagą (at). Apibendrinant, iš elastingumo santykių (5) įtempį išreiškiame deformacijos reikšme. Pirmąjį iš santykių (5) parašykime formoje
Naudodami lygybę (9) turėsime
Panašius ryšius galima išvesti ir . Kaip rezultatas, mes gauname
|
Čia mes naudojame santykį (8) šlyties moduliui. Be to, pavadinimas
POTENCIALI ELASTINIO DEFORMACIJOS ENERGIJA
Pirmiausia panagrinėkime elementarų tūrį dV=dxdydz vienaašių įtempių sąlygomis (1 pav.). Psichiškai sutvarkykite svetainę x=0(3 pav.). Jėga veikia priešingą paviršių .
Ši jėga veikia poslinkį .
Kai įtampa didėja nuo nulinio lygio iki vertės
atitinkama deformacija dėl Huko dėsnio taip pat didėja nuo nulio iki reikšmės ,
ir darbas yra proporcingas tamsintai figūrai pav. 4 kvadratai: 
. Jei nepaisysime kinetinės energijos ir nuostolių, susijusių su šiluminiais, elektromagnetiniais ir kitais reiškiniais, tai dėl energijos tvermės dėsnio atliktas darbas virs potencinė energija, susikaupę deformacijos metu: .
Vertė Ф= dU/dV paskambino specifinė potenciali deformacijos energija, turinčios kūno tūrio vienete sukauptos potencinės energijos reikšmę. Esant vienaašiai įtempių būsenai
